从博弈论的角度分析诈唬(2)：特殊情况中的期望回报
从博弈论的角度分析诈唬(2)：特殊情况中的期望回报
第一篇文章请点击这里：
从博弈论的角度分析诈唬(1)：什么情况下该诈唬
今天，我们要说的是第三点：
一些特殊情况下的期望回报下面两张表显示了特殊情况中的期望回报。
第一张图表示的是听牌失败时的期望回报，用上一篇文章的例子来计算：
对手的期望回报是你的期望回报的负数，再加上已经在底池中的$100。
他会得到你在下注轮的净损失+现有底池。当然如果你赢下底池的话，你的净损失是– $100，他没有回报。
来看看最简单的情况：当你的期望回报是0时，你的筹码量不会发生变化，因此你不会赢下底池，底池会被对手赢走。由于我们已经玩到河牌圈，所以这不是一个零和博弈。
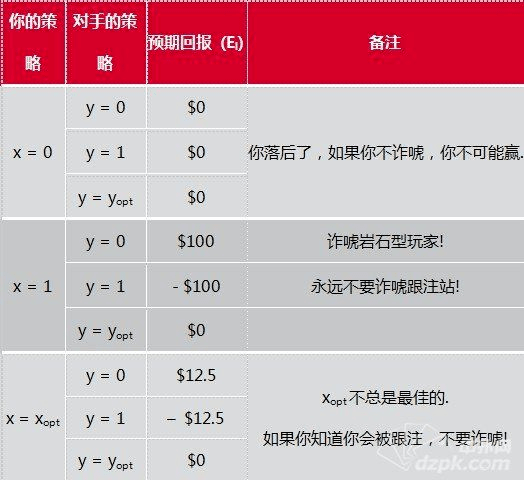
如果你知道什么时候诈唬，什么时候价值下注，而对手却不知道，对他来说(也可能是对你)，下面的这个图表会更有用。
这张表显示的是综合获胜和失败之后，你的期望回报。我们假设过，你有20%的时候领先，80%的时候落后，因此你的平均期望回报是 qEw + (1 – q)El。(这个结果的负值+底池现有的$100=对手的期望回报Eop。)
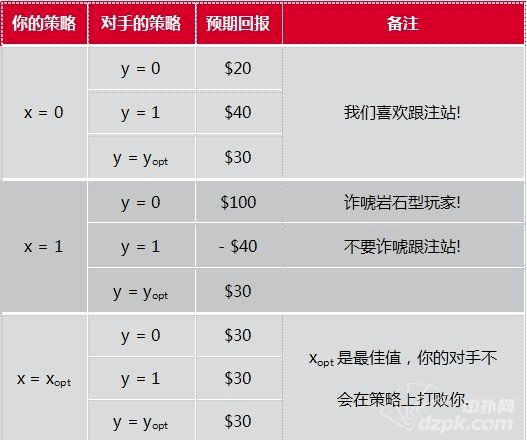
结论当你面对优秀的对手时，最好的选择就是利用纳什均衡点为你提供的策略：xopt。在这种情况对手会用 yopt的策略打牌。如果他没有使用，他就在犯错(也说明他不是一个优秀的玩家)，你就可以利用他的错误找到最佳的打法。
如果他经常跟注，你就少诈唬，如果他很少跟注，你就多诈唬。如果你能猜到他的跟注频率，就可以根据期望回报最大化的原则，计算自己应该诈唬的频率。
附录◆◆yopt是怎样计算的◆◆如果y = yopt，无论x是多少，你的期望回报都不会改变。让我们先假设x = 0，这时你什么牌也赢不了，公式是：
El = 0
现在假设x = 1，El的公式变为
El = (1 – yopt)P – yoptB
因为x=0和x=1时的期望回报一样，所以
(1 – yopt)P – yoptB = 0,
所以
(1 – yopt)P = yoptB,
P – yoptP = yoptB,
P = yopt(P + B),
最后
yopt = P/(P + B)
◆◆从对手的角度来看◆◆现在我们从对手的视角看看这个问题。
首先我们要列出他的期望回报Eop。由于他不知道你的牌是领先还是落后，所以他的期望回报还会受到q的影响，所以这个公式会复杂一点：
Eop = – qyB + q(1 – y)0 + (1 – q)xy(P + B) + x(1 – y)0 + (1 – x)P
– qyB 表示你有优胜牌，你下注，他跟注，并且输了。
q(1 – y)0表示你有优胜牌，但是他弃牌，没有输赢。
(1 – q)xy(P + B) + x(1 – y)0 + (1 – x)P是他领先时的情况。
方括号中xy(P + B)表示你诈唬，他跟注，他赢得底池和你的下注。
x(1 – y)0 表示你诈唬，他弃牌，没有盈利和损失。
(1 – x)P表示你弃牌，他赢下底池的情况(包括他过牌赢下摊牌和他下注你弃牌两种情况)
省略其中为0的部分，我们得到
Eop = (1 – q)xy(P + B) + (1 – x)P – qyB
如果对手知道你从不诈唬(x = 0)，那他的最佳打法是什么？他永远不会跟注，在上面的公式中如果用0代替x，我们得到
Eop x=0 = (1 – q)P– qyB
为了使结果最大化，我们必须让y = 0 (永远不跟注)。
反过来，如果对手知道你总是诈唬(x = 1)，那他就很难找到最佳应对方式了。如果x = 1，我们得到
Eop x=1 = (1 – q)y(P + B) – qyB = y(1 – q)(P + B) – qB
如果
(1 – q)(P + B) – qB > 0,
y = 1 (总是跟注)会让对手的期望回报最大化。
如果
(1 – q)(P + B) – qB < 0,
他就应该使用 y = 0 (永远不跟注)的策略。
(1 – q)(P + B) – qB < 0
意味着
(1 – q)(P + B) < qB,
P + B – qP – qB < qB,
P + B < q(P + 2B),
最后
q > (P + B)/(P + 2B)
在我们的例子中，P = B = $100，如果q > 2/3，对手应该永不跟注(即使他知道你总是下注;因此在这种情况中你总是应该诈唬)， 当q < 2/3时，他应该总是跟注(如果他知道你总是诈唬)。记住，这个q的值也仅取决于底池大小和下注大小。
◆◆xopt是怎么计算的？◆◆如果x = xopt，那么无论y是多少，对手的期望回报都不会改变。和之前一样，先假设y = 0。Eop的公式为
Eop = (1 – q)(1 – xopt)P
现在假设y = 1，我们得到
Eop = (1 – q) xopt (P + B) + (1 – xopt)P – qB
因为y=0和y=1时的Eop一样，我们得到
(1 – q)(1 – xopt)P = (1 – q) xopt (P + B) + (1 – xopt)P – qB,
因此
qB = (1 – q) xopt (P + B)
(两边都有(1 – q)(1 – xopt)P，因此可以消掉)，所以最终我们得到
xopt = qB/(1 – q)(P + B)
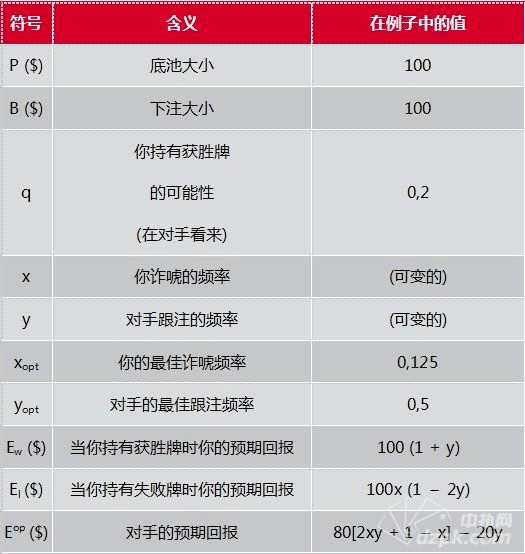
当我们讨论频率时，我们通常用 0.2代替20%，用0.5代替50%等等。一件不可能的事件发生的可能性是0 (0%)，一件确定的事发生的可能性是1 (100%)。剩下的其他事件发生的可能性在0和1之间。https://www.moshike.com/
FAQ
什麼是微撲克長效簽名包？
什麼是長效簽名包？ 微撲克長效簽名包可在iPhone、iPad下載，與普通版相比，可以有效減少軟件頻繁授權簽名次數，服務由第三方提供，有效期內
微撲克軟件下載安裝後無法打開或閃退，怎麼辦?
微撲克軟件下載安裝後無法打開或閃退，怎麼辦? 您只需先卸載已安裝的微撲克app，在微撲克下載頁面安裝即可解決。 微撲克普通版 ：應用下載安裝後，在
