我学会了用强化学习打德州扑克
我学会了用强化学习打德州扑克
最近,强化学习(RL)的成功(如 AlphaGo)取得了大众的高度关注,但其基本思路相当简单。下面我们在一对一无限注德州扑克游戏上进行强化学习。为了尽可能清楚地展示,我们将从零开始开发一个解决方案,而不需要预设的机器学习框架(如 Tensorflow)。让我们用 Python3 Jupyter notebook 开始吧!
- 问题设置
- 强化学习
- 特征:
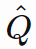 的输入(下文使用 Q^表示 Q hat)
的输入(下文使用 Q^表示 Q hat) - 关于 Q^ 的线性模型
- 模拟扑克游戏
- 学习:更新 Q^
- 整合
- 结果
- 解释模型
- 可视化策略
- 结语
问题设置
规则提醒:该游戏是一个 2 人无限注的德扑游戏,其中:
1. 游戏开始,两名选手均有 S 筹码和随机发放的 2 张底牌。
2. BB(大盲注)玩家下 1.0 个盲注,SB(小盲注)玩家下 0.5 个盲注。
3. 小盲注玩家可以全押(all-in)或弃牌(fold)。
4. 如果小盲注玩家全押,那么大盲注玩家可以跟注(call)或弃牌。
我们可以将规则可视化为下图所示的决策树。游戏开始于 E,这时 SB 可以全押或弃牌。如果他弃牌,我们转移到状态 A,游戏结束。如果他全押,我们转移到状态 D,BB 必须在跟注和弃牌之间作出决定。如果一个玩家弃牌,另一个玩家就会得到盲注,如果两个玩家全押,则发放 5 张公共牌,并且金额按照扑克的正常规则进行分配。
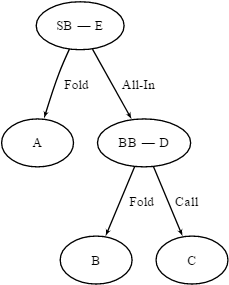
这个游戏有著名的的解决方案,也有其它的方法,如虚拟对局和直接优化。这里,我们将使用强化学习估算解决方案。
这里有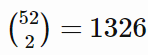 种不重复的 2 张手牌组合数。因此,我们可以给所有牌排序,并从 0 到 1325 编号。只要前后编号一致,具体的顺序就不重要了。以下函数隐含地定义了这样一个排序,并创建了从牌的编号到相关决策信息的映射:牌的排序(牌面顺序/rank)和同花性(牌面花色/suitedness)。
种不重复的 2 张手牌组合数。因此,我们可以给所有牌排序,并从 0 到 1325 编号。只要前后编号一致,具体的顺序就不重要了。以下函数隐含地定义了这样一个排序,并创建了从牌的编号到相关决策信息的映射:牌的排序(牌面顺序/rank)和同花性(牌面花色/suitedness)。

请注意,输出元组中的第一个元素(代码中的 r2)始终排序靠前,如果有的话。例如,手牌编号 57 恰好是 6♦2♣,我们有:

当玩家全押时,他们平均获得的底池(「期望利益」)根据游戏规则决定。文件 pf_eqs.dat(http://willtipton.com/static/pf_eqs.dat)包含一个 numpy 矩阵 pfeqs(http://docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.savetxt.html),其中 pfeqs i,j 指当对手持有手牌 j 时持有手牌 i 的期望利益。
当然,有时候两人起始手牌有一张牌是相同的,在这种情况下,它们的期望不能同时计算,这时取得他们的期望利益也不合适。文件 pf_confl.dat(http://willtipton.com/static/pf_confl.dat)包含另一个 1326×1326 矩阵,其中每个元素为 0 或 1。A 0 表示两位玩家的起始手牌不一样,a 1 表示起始手牌一样。

例如,由于手牌 56 是 6♦2♣,57 是 6♥2♣,58 是 6♣2♠,于是我们有:
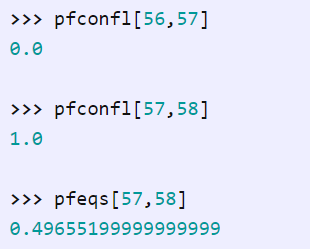
为什么结果不正好是 0.5 呢?
强化学习
下面进入 RL 教程。RL 问题有三个重要组成部分:状态(state)、动作(action)、奖励(reward)。它们合在一起如下:
1. 我们处于某「状态」(即我们观察到的世界的状态)。
2. 我们使用这个信息来采取某「动作」。
3. 我们会得到某种「奖励」。
4. 重复以上过程。
一遍又一遍地重复以上过程:观察状态、采取行动、获得奖励、观察新的状态、采取另一个行动、获得另一个奖励等。RL 问题只是找出如何选择行动的方案以获得尽可能多的奖励。事实证明这是一个非常普遍的框架。我们可以通过这种方式考虑许多问题,解决这些问题也有很多不同的方法。一般来说,解决方案涉及随机游走(wandering around),在不同状态选择各种行为,记住哪些组合能够获得什么奖励,然后尝试利用这些信息在未来做出更好的选择。
RL 如何用于德扑游戏呢?在任何决策点上,玩家知道他的 2 张底牌和他的位置,这就是状态。然后他可以采取行动:要么弃牌,要么 GII。(GII 对于 SB 意味着全押(shove),对于 BB 意味着跟注)。然后得到奖励——这是玩家赢得的钱数,在最后的手牌中我们将使用玩家的总筹码大小。例如,如果初始筹码大小为 S=10,SB 全押 BB 弃牌,则玩家的奖励分别为 11 和 9。
我们会通过模拟手牌组合来找到游戏的策略。我们会同时处理两个玩家的随机手牌,让他们做出关于如何玩的决策,然后观察他们每次结束时最终得到多少钱。我们将使用该信息来学习(估计)Q 函数 Q(S,A)。Q 的参数为状态 S 和动作 A,输出值为在该状态下采取该动作时得到的最终奖励值。一旦我们有 Q(或它的某种估计),策略选择就很容易了:我们可以评估每个策略,看哪一个更好。
所以,我们这里的工作是估计 Q,我们将使用 Q^(发音为「Q hat」)来指代这个估计。初始化时,我们将随机猜测一些 Q^。然后,我们将模拟一些手牌,两名玩家根据 Q^ 做出决定。每次手牌之后,我们将调整估计值 Q^,以反映玩家在特定状态下采取特定动作后获得的实际值。最终,我们应该得到一个很好的 Q^ 估计,这就是确定玩家策略所需的所有内容。
这里需要注意一点——我们要确保在所有状态采取所有动作,每个状态-动作组合至少尝试一次,这样才能很好地估计出最终每个可能的值。所以,我们会让玩家在一小段时间ε内随机地采取行动,使用他们(当前估计的)最佳策略。首先,我们应该积极探索选择的可能性,频繁地随机选择。随着时间的推移,我们将更多地利用我们获得的知识。也就是说,ε将随着时间的推移而缩小。有很多方法可以做到这一点,如:

Q 被称为「动作价值函数(action-value function)」,因为它给出了采取任何特定动作(从任何状态)的值。它在大多数 RL 方法中有重要的作用。Q^ 如何表示?如何评估?是否在每次手牌之后更新?
特征:Q^ 的输入
首先,Q^ 的输入:状态和动作。将这个信息传递给 Q 函数,作为位置(比如,SB 为 1,BB 为 0),手牌编码(0 到 1325),动作(比如,GII 为 1,弃牌为 0)。不过,我们将会看到,如果我们做更多的工作,会得到更好的结果。在这里,我们用 7 个数字的向量描述状态和动作:

由函数 phi 返回的向量φ将是 Q 函数的输入,被称为特征向量,各元素都是特征(φ发音为「fee」)。我们将看到,我们选择的特征可以在结果的质量上产生很大的不同。在选择特征(称为「特征工程」)中,我们利用了有关问题的相关领域知识。它和科学一样艺术化。在这里,我们将判断哪些为相关信息(在这种情况下)的知识用以下几种方式编码。让我们来看看。
为方便起见,第一个元素始终为 1。考虑接下来的四个元素。这些代表玩家的手牌。我们已经从手牌编码转换为 rank1、rank2 和 isSuited。这三个变量技术上给出与手牌编码相同的信息(忽略特定的组合),但是该模型将更好地利用这种格式的信息。除了原始排序,我们还包含了 (|rank1-rank2|)^0.25。我们碰巧知道 connectedness 是德扑的重要属性,正如其名。此外,如果所有特征都量纲一致,该模型的学习效果会更好。在这里,所有的特征大致介于 0 和 1 之间,我们通过将 rank 除以 numRanks 得到。
最后,如果 not isGII(即如果动作是弃牌),我们实际上将这些数字设置为 0。我们知道,当玩家弃牌时,特定的持有手牌对结果没有任何影响(忽略小概率的卡牌移除效果),所以我们在这种情况下删除无关的信息。
现在考虑最后两个元素。第一个直接编码玩家的位置,但第二个同时取决于 isSB 和 isGII。为什么会这样?稍后我们会显示这个「交叉项」的必要性。
关于 Q^ 的线性模型
我们将学习一个线性函数用于估计的 Q^ 函数。这意味着我们将真正学习一个参数向量,通常称为θ,它的长度(7)与特征向量相同。然后,我们将针对特定的φ来估计 Q^ :
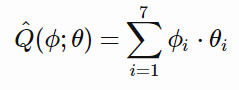
这里,下标 i 指代向量的特定元素,并将参数列表写为 (φ;θ),其表示 Q^ 的值取决于φ和θ,但是我们可以认为是φ的函数,θ为固定值。代码很简单:

虽然这个函数普遍使用,但是这个算法没有什么特别之处,以使它成为这个问题的最佳选择。这只是其中一种方法:将某些学习参数与某些特征相结合以获得输出,并且完全由我们定义一个θ向量,使它产生我们想要的输出。然而,正确选择θ将为我们很好的估计在有特定的手牌时采取特定行动的价值。
模拟扑克游戏
我们接下来要「玩」手牌了。我们将在接下来的几个部分中进行,不过现在我们先构建三个重要的概念。这些概念与 RL 问题的三个重要组成部分相关:状态、动作和奖励。首先,状态——每次手牌,我们将以随机发牌的方式初始化每个玩家的状态。

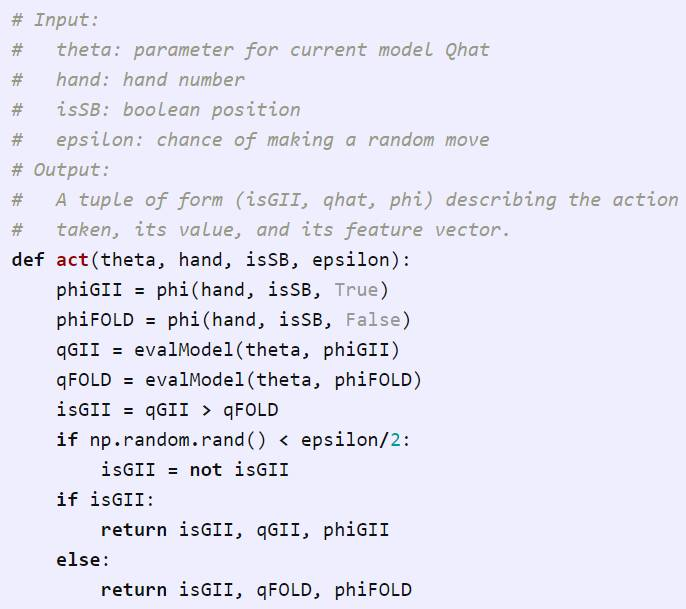
第二点,采取动作。每个玩家将使用当前的模型(由 theta 给出)和已知的手牌和身份(为 SB)来选择动作。在以下函数中,我们估计 GII 和弃牌/FOLD(qGII 和 qFOLD)的值。然后选择当下的最优项(1-ε),否则随机选择动作。返回所采取的动作,以及相应的价值估计和特征向量,这两项我们之后会用到。
第三点,一旦我们知道每个玩家当下的手牌和动作,我们就模拟剩下的手牌来得到玩家的奖励。如果任何一个玩家弃牌,我们可以立即返回正确的奖励值。否则,我们参考玩家的状态和奖励期望(equity),在正确的时间段随机选择一个赢家。
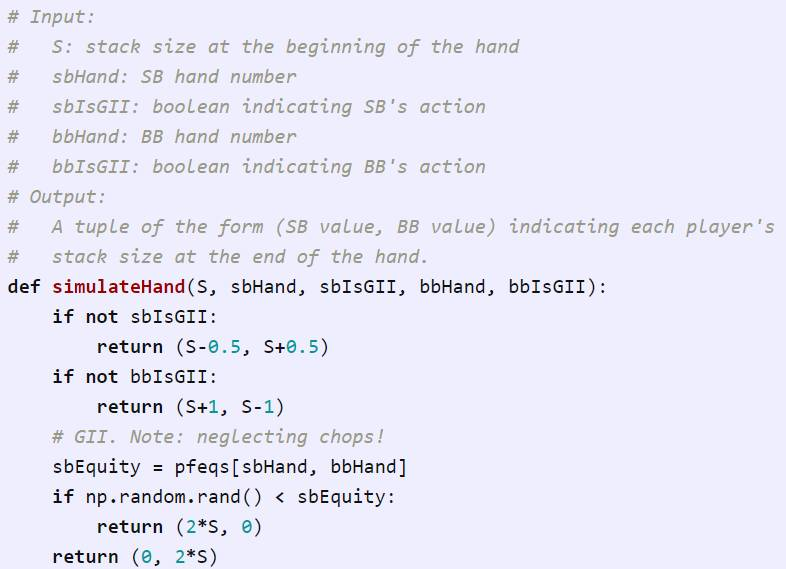
在玩家全押的情况下,我们用小技巧规避了模拟。与通过使用 5 张公共牌实际模拟游戏并评估玩家的手牌来查看谁赢不同,我们现在根据预先计算的概率随机选择一个赢家。这在数学上是等价的(琐碎的证明忽略);这只是一个更方便和更有计算效率的方法。
最重要的是,我们的学习过程没有利用这些 equity 或有关游戏规则的信息。正如我们马上将要看到的那样,即使是完全模拟,学习过程也没有什么不同,甚至 智能体(agent)还会与外部黑盒的扑克游戏系统进行交互从而可能遵循不同规则!那么,学习过程究竟如何进行?
学习:更新 Q^
一次手牌结束之后,我们需要更新 theta。对于每个玩家,我们已知其状态和采取的动作。我们还有动作对应的估计价值以及从游戏中获得的实际奖励。从某种意义上说,实际获得的奖励是「正确解」,如果动作的估计价值与此不同,则我们的模型有误。我们需要更新 theta 以使 Q^(φ;θ) 更接近正确的答案。
令 φ' 为一个玩家所在的特定状态,R 是她获得的实际奖励。令 L=(R-Q^(φ;θ))^2。L 被称为损失函数。L 越小,R 越接近 Q^(φ;θ),如果 L 为 0,则 Q^ 恰好等于 R。换句话说,我们想要微调整 θ,使 L 更小。(注意,有许多可能的损失函数,使得随着 Q^ 越来越接近 R,L 越来越小。这里的损失函数只是一个常见的选择)。
所以「更新 Q」是指改变θ使 L 更小。有不止一种方法可以做到这一点,一种简单的方法为随机梯度下降(stochastic gradient descent)。简而言之,其更新 θ 的规则是:
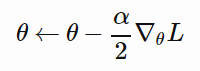
我们需要选择「超参数」α(称为学习率),它能控制每次更新的幅度。如果α太小,学习速度很慢,但是如果它太大,则学习过程可能无法收敛。将 L 代入到这个更新规则,并进行几行微积分计算,我们得到
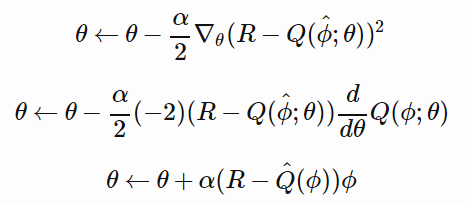
最后一行提供了更新参数的准则,我们将依此编写代码。注意这里的 θ 和 φ 都是长度为 7 的向量。这里更新参数的准则分别适用于每个元素。
整合
最后,该整合所有内容了。重复以下步骤:
1. 随机发给每个玩家手牌。
2. 令玩家各自选择一个动作。
3. 得到结果。
4. 使用观测到的(状态,动作,结果)元组更新模型。
下面的函数 mc 实现了这种蒙特卡罗算法,并返回学习模型的参数 theta。

特别注意,上节推导出的参数更新规则在代码中得到了实现。
结果
解释模型
本例中,固定 S=10。

我们得到了数字,但是它们有意义吗?实际上有几种方法可以帮助我们判断,并通过它们得到一些模型的解释。
首先,我们考虑某些具体的情况。当 SB 弃牌(FOLD)时,它的估计值是多少?很容易得到,因为在这种情况下 φ 比较简单。实际上,除了第 1 个(固定为 1)和第 6 个(对应于 isSB)之外,所有元素都为 0:phi = 1,0,0,0,0,1,0。所以,我们的线性模型的 Q^ 仅相当于加总 theta 的第 1 个和第 6 个元素:
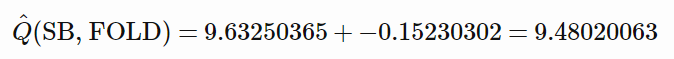
现在我们知道,根据游戏的规则,SB 选择弃牌的价值是 9.5。所以,非常酷,模型与真实情况非常接近!这是一个很好的逻辑判断,并用例子说明了如何估计我们模型可能的误差值大小。
另一种情况:BB 弃牌。只有 phi 的第 1 个元素是非零的,我们发现一个估计值
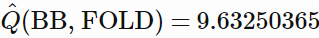
虽然不清楚正确的答案应该是什么,除了知道它肯定应该在 9(如果 SB 总是 GII)和 10.5(如果 SB 总是弃牌)之间。事实上,这个数字更接近 9 而不是 10.5,这与 SB 更倾向于 GII 而不是相一致。
有一个更一般的方法来思考每个 θ 输入。每个元素 θ_i 都会造成 Q^ 的增加,因为对应的特征 φ_i 会增加 1。例如,当有合适的手牌同时执行 GII 策略时,θ 的第 5 个元素会增加 1。因此,有适合手牌的估计奖励值是 0.22571655——一个小的正向奖励。看上去是合理的。
θ 的第 2 个元素(对应于玩家排名较高的手牌)是 6.16764962。这对应于特征:如果 isGII 则为 rank2/numRanks,否则为 0,意思为玩家排名较高手牌时的 GII 策略。这里 rank2 除以 numRanks,所以特征每增加 1 约等于 2 和 ace 之间的差。以一个额外的 6 BB 加上 1 个 ace 而不是 2 来取得胜利似乎是合理的。(但是,为什么你会觉得有第二张更高的手牌显然是负的?)
检查与第 6 个特征相对应的 θ 的元素(如果 isSB 则为 1,否则为 0),如果所有其它特征相等,则在 SB 中的附加值显然为-0.15230302。我们或许可以把这解释为位置上的劣势:由于不得不首先采取行动的小惩罚。
然而,其它一切并不一定相同。如果 SB 执行 GII 策略,则最后一个特征也非零。所以,-0.15230302 为 SB 执行弃牌时的附加值。当执行 GII 时,我们总结最后一个特征的贡献,发现奖励为-0.15230302 + 0.14547532 = -0.0068277。显然,当 SB 采取更激进的策略时,位置劣势就变少了!
我们在这里看到,在本问题范畴内,选择有意义的特征可以帮助我们有效地解释结果。有趣的是,有一个被称为 SAGE 的老规则来玩德扑游戏。这个规则在锦标赛现场容易被记住。原则是为你的手构建「能力指数」,它按照顺子(rank)、同花(suitedness)和对子(pair)进行规则构建,然后用它来决定是否 GII。它们的特征组合与我们的特征组合相比如何?它们的结果怎么样?
最后,为什么我们选择 isSB 和 isGII 来决定最后一个特征,而不仅仅是 isGII?思考如下。(BB,FOLD)的估计值只是 θ 的第 1 个元素,所以这个第 1 个元素需要能够随意变化,以获得正确的(BB,FOLD)值。那么,第 6 个元素是在 SB 中的额外贡献,它需要能够随意变化以获得正确的(SB,FOLD)。
一旦我们从弃牌转换到 GII,元素 2-5 变为非零状态,并根据玩家调整为特定值,但这些决策同样适用于 SB 和 BB。该模型需要为 SB 全押提供一些不同于 BB 全押的决策。
假设我们的最终特征为:如果 isGII 则为 1,否则为 0。这不取决于玩家,所以 SB 和 BB 的估计值之间的唯一差异将在于 isSB 项。这个数字必须考虑在执行弃牌时 SB 和 BB 之间的差异,以及在执行 GII 时 SB 和 BB 之间的差异。模型必须在这两个差异之间挑选一个数字,最终可能会导致一些差的折中。相反,我们需要:如果 isGII 和 isSB 则为 1,否则为 0。这样,该模型可以区分 SB GII 与 BB GII 的增量值。
注意,该模型仍然无法捕获很多细微的细节。例如,由于模型完全内置的函数形式,我们看到的 GII 的估计值的差异在两个特定手牌组合下,如 A2 和 K2,对于 SB 和 BB 是完全相同的。不管θ的值如何,我们的模型都不可能预测。
这样的模型有很高的偏差值(bias)。它是不灵活的,并且有一个强大的内置「观点」来决定结果将是什么样子。这就是为什么特征工程如此重要。如果我们没有尝试为算法提供精心设计的特征,那么它或许就没有能力表征一个很好的解决方案。
可以为模型添加更多的特征,如其它交叉项,以获得偏差较低的模型,但这可能会带来缺点。这会很快失去可解释性,也可能会遇到更多的技术问题,比如过拟合。(当然,在多数使用中这并不是首要问题,准确性比可解释性更重要,而且有办法处理过拟合)。
可视化策略
要找到完整的策略,我们将评估该模型,以了解在每个玩家的 1326 种手牌组合中,GII 或弃牌哪个更好:

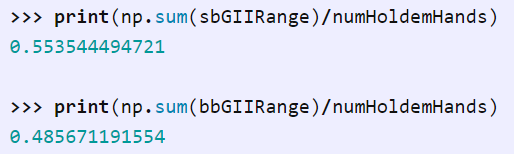
看上去,对于 SB,大约 55%的手牌选择全押,而对于 BB,大约 49%的时间选择跟注:
最后,我们可以生成一些 SVG 来在 Jupyter 环境中绘制 GII 范围:


我们怎么选择呢?这里有我们期望的很多定性的特征:大的手牌很好、有对子很好、同花好于不同花、SB 比 BB 打法松等。然而,边界线(borderline)手牌的打法有时候会与在真正的平衡策略中不同。
结语
这篇介绍性的应用 RL 技术的文章给我们提供了一些合理的策略来进行德扑游戏。该学习过程不依赖于任何结构或游戏规则。而是纯粹地通过让智能体自己进行游戏、观察结果,并根据此来做出更好的决定。另一方面,重要特征工程需要一些领域专业知识才能学习一个好的模型。
最后,介绍一些背景。许多合适的问题都可以阐述为 RL 问题,也有许多不同的方法来解决它们。这里的解决方案可能具有以下特征:无模型(model-free)、基于价值的(value-based)、蒙特卡罗(Monte Carlo)、在策略(on policy)、无折现型(undiscounted),并使用线性函数逼近器(linear function approximator)。
- 无模型:agent 通过采取行动和观察奖励来学习。它不需要任何关于如何产生这些奖励的先验知识(例如关于诸如范围、权益、甚至游戏规则),也没有试图匆忙地学习这些东西。在扑克游戏中,事实上我们很了解某些手牌和动作能导致何种特定奖励(我们可以利用这一点),但是在许多其它情形中并不是这样。
- 基于价值的:我们专注于找出每个状态下每个动作的价值,然后确定实际的策略,这或多或少是事后想法。还有基于策略的方法(如虚拟游戏),其重点是直接学习在每个状态采取的动作。
- 蒙特卡罗:我们对整个手牌组合(情节)进行抽样,并根据我们在手牌后获得的价值进行学习。「时序差分(temporal difference)」方法可以在手牌结束之前对所有中间状态的预期值进行估计,并且可以更有效地利用这些值来学习。考虑到每个玩家在结束之前只能在德扑游戏中进行单一动作,虽然这对我们来说并不重要,但它可以在更多的状态的问题上产生很大的影响。
- 在策略:我们估计玩家策略的价值。实际上这并不简单。因为玩家有时候会采取随机(非最优)的动作,所以我们估计的价值不是最优策略的值,这不是我们真正想要的。即使在探索非最优选择的同时,更为复杂的「离策略(off policy)」方法也可以了解实际的最优策略。
- 无折现型:大多数 RL 问题从始至终包含很多(可能无限多)状态。当然,在这种情况下,agent 希望最大化所有未来奖励的总和,而不是最大化即刻奖励。在这种情况下,假设相对于将来的某个时间获得奖励,agent 对于当下获得奖励的偏好较小。德扑游戏的一局手牌时间总是很短,所以我们不需要担心。
- 线性函数逼近器:本例中学习的是一个线性函数,它将(状态-动作)对的表征映射到数值。其它替代方法包括简单的表(它将每个状态的每个动作的估计数值单独存储),以及许多其它类型的函数逼近器。特别地,这种方法在神经网络中非常成功。在某种程度上,这是因为它们不需要很多特征工程来获得好的结果。神经网络通常可以学习一组好的特征,以及学习到如何使用它们!但本文暂不探讨这个话题。
FAQ
德州一般几个人?
一副标准扑克牌去掉大小王后的52张牌进行游戏。 一般2-10个玩家,个别情况有12个玩家的。 玩家之间同时继续看牌或比牌需要下同样注额筹码,筹码
美国德州扑克合法吗?
根据美国联邦法律,赌博是受法律限制的。 各个州对于各种类型的赌博的限制程度都不同。 广受全世界人民欢迎的“德州扑克”却在德州是违法的。 除了慈善用
德州扑克一般几个人玩?
一副标准扑克牌去掉大小王后的52张牌进行游戏。 一般2-10个玩家,个别情况有12个玩家的。 玩家之间同时继续看牌或比牌需要下同样注额筹码,筹码
德州扑克在中国违法吗?
在中国,德州扑克被列为违法赌博,且无中国国家体育总局的批准,不是中国认可的竞技类棋牌运动。
微撲克軟件下載安裝後無法打開或閃退,怎麼辦?
微撲克軟件下載安裝後無法打開或閃退,怎麼辦? 您只需先卸載已安裝的微撲克app,在微撲克下載頁面安裝即可解決。 微撲克普通版 :應用下載安裝後,在


























































